Волновые топологии в календаре майя

Календарь Майя является таким текстом, который ведет себя как голографическая пленка, в которой закодирована информация, которую можно разблокировать, если у вас есть ключ/код

Я считаю, что многие священные и древние тексты/рукописи/диаграммы демонстрируют голографическое качество, поскольку они представляют собой небольшие части более широкой реальности с достаточным количеством ключевой информации, которая позволила бы ее в некотором смысле реконструировать или пройти через фильтр восприятия, который позволил бы вид более полной системы, если вы посмотрите на нее достаточно долго.

http://jellobrain.com (орфография сохранена)

Я сосредоточил свою работу конкретно на базовом календаре «Цолькин», который, по сути, составляет один из 16 «месяцев» (по 260 дней каждый) солнечного цикла (~ 11,2). лет по земному времени).

Мое знакомство с календарем

Когда я впервые начал изучать календарь, я просматривал некоторые работы Хосе Аргуэлеса. Я считаю, что академия пыталась уничтожить роль воображения в знании, называя его дезинформацией, и что на каком-то уровне его работа стала жертвой того, что ученые не понимали природу получения информации так, как он.  

Несмотря на мое уважение к его работе, я отступаю от предложенной им конфигурации 8-ми решетчатой ??матрицы Цолькина в одном важном отношении, которое вы увидите ниже.

Использование математики как языка для интерпретации календаря

По сути, если вы поручите 10 специалистам по алгебраическим топологиям и попросите их изучить календарь Цолькина, то он сможет представлять брану (иш) в смысле этих топологий и их связей с тканью реальности.

В какой-то момент я решил сосредоточиться исключительно на сетке (13X20) как математической сущности.

Здесь я отхожу от работы Аргуэлеса по расположению сложенных друг на друга сеток. В концепции Аргуэлеса он переворачивает сетку один раз по вертикальной оси и один раз по горизонтальной оси. Я хотел посмотреть, что произойдет, если вы просто перевернете сетку один раз по горизонтальной оси, а затем соедините их вместе, как батарею.

Выше вы можете видеть, что нижние четыре Цолькин и верхние четыре Цолькин не являются Зеркалами. 

В Пси-банке Аргуэлеса верх и низ перевернуты ОБА по горизонтали и по вертикали. В своей работе, хотя я также тестировал набор Аргилеса, я решил перевернуть сетку только по горизонтали.

Создание кода для интерпретации матричных сеток

Я создал программу для анализа всевозможных вариантов того, что происходит, когда матрица/сетка соединяется вместе с их различными зеркалами различными способами. 

Она все еще находится в зачаточном состоянии, но я хотел представить её, чтобы вы могли следить за тем, что я говорю и экспериментировать с этим, если хотите. Я также прилагаю несколько рисунков и хочу объяснить, что я здесь сделал.

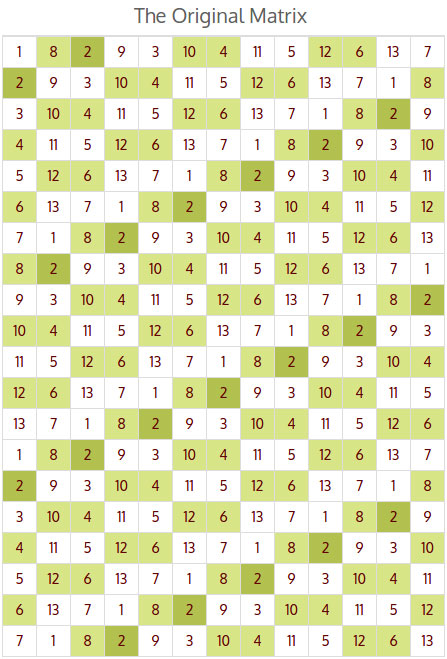
Календарь Цолькин представляет собой сетку 13x20, в которой каждый начинает с верхнего левого угла и считает от 1 до 13, двигаясь вниз по столбцам, а затем вправо, снова и снова 20 раз, так что всего имеется 13 столбцов с 20 рядов. 

Я рассматривал математические отношения в этой сетке как отдельную единицу, а также в более крупной матрице четверти (4 Цолькин) и половины (8 Цолькин) солнечных циклов.

Во-первых, большая часть информации, с которой работал, содержится в полученной аналогичным образом матрице 15x3 в mod 9 (чертежи также прилагаются ниже), с которой я тоже экспериментировал.

Во-вторых, если вы «отражаете» любую из матриц сами на себя (фотографии ниже), соединяя их синкопированным образом, порядок матрицы обогащается, а отношения чисел в этой «зеркальной» матрице обогащаются и кажется, содержат рецепты тороидальной системы, которую описывает матрица.

Третий принцип является связующим звеном.
Преобразование между моей объединенной матрицей, по сути, представляет собой ситуацию типа «сводной таблицы». 

Посмотрите на матрицы с основанием 9, которые вы создаете, и представьте, что вместо того, чтобы смотреть на них как на сетку квадратов, вы поворачиваете их на 45 градусов и смотрите на них как на ромбовидную сетку. По сути, ромбовидную сетку можно рассматривать как две соединенные вместе сетки. Соответствующие сетки соединяются не линиями, а точками. 

Таким образом, исходная сетка, составляющая календарь майя, например, при соединении ее с зеркалом создает матрицу, очень похожую на те, которые  используются для определения моделей тороидальной энергии.

Во-вторых, исходная сетка Vortex AHBA (mod9) имеет третье число, которое определяет высоту сетки, так что это число больше не связано со вторым числом матрицы (в данном случае 9, нумерация mod9).

И в-третьих, в сетках, которые используются, сращивание смещено, как показано в видео, которое я создал, чтобы проиллюстрировать свою точку зрения ниже:

Основная идея заключалась в соединении сетки и ее зеркального отражения в более крупную чередующуюся сетку.

Я обозначил две соединенные вместе сетки, придав каждой из них разный цвет, который вы можете увидеть в первой серии сеток.

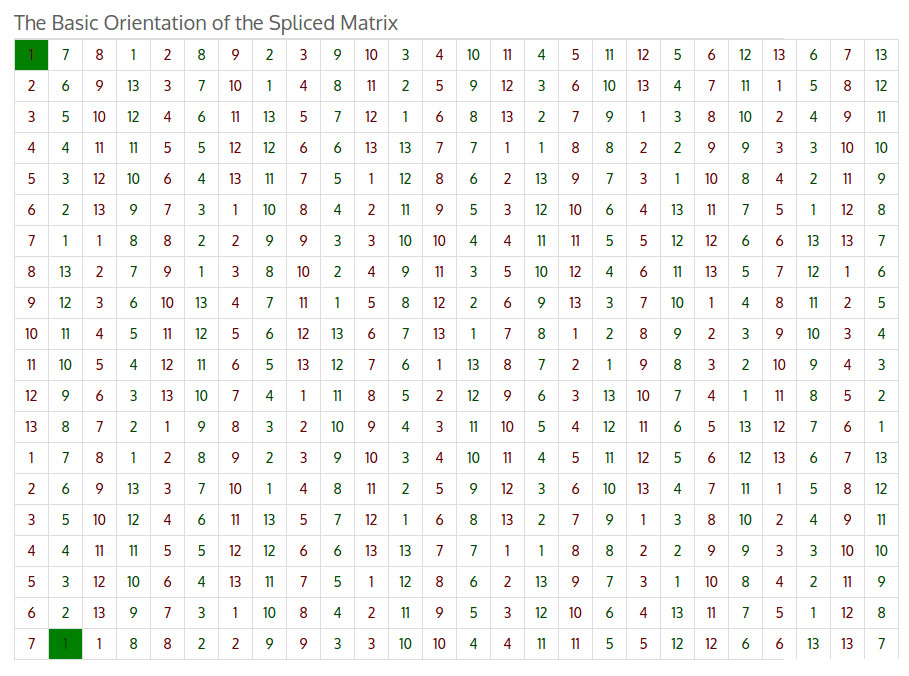
Приведенный выше инструмент построения и оценки матрицы берет эту склеенную сетку и снабжает ее сильными лекарствами (?).

Более конкретно, когда я смотрел на различные шаблоны чисел в сетке, я заметил, что шаблоны, созданные нечетными и четными числами, похоже, соответствуют строкам, в которых есть повторяющиеся соседние числа.

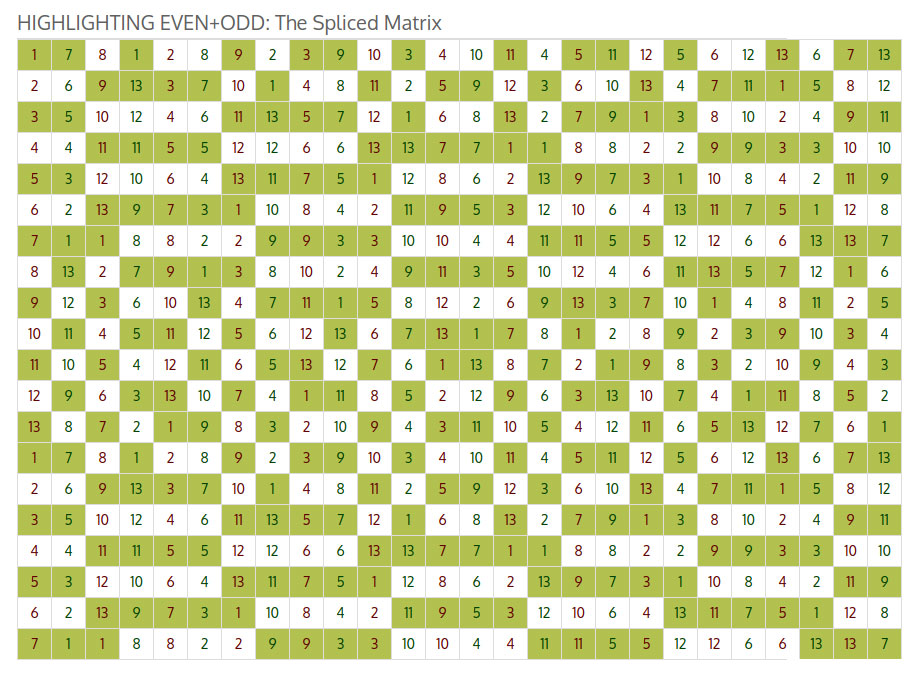
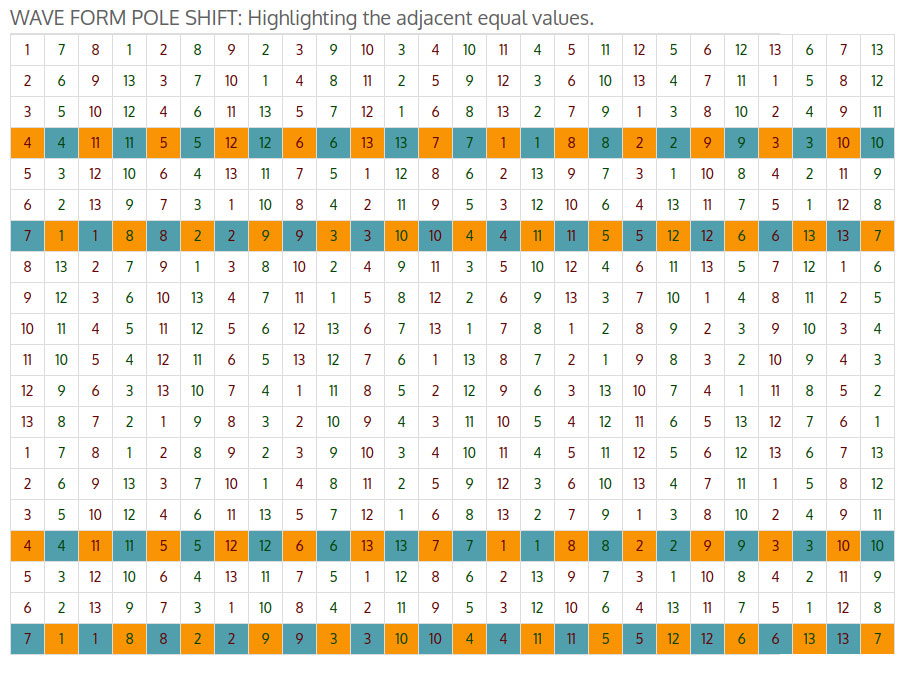
Затем я провёл некоторые расчеты и понял, что в музыке существует понятие «масштаба». Верхняя строка исходной матрицы содержит ряд повторяющихся чисел в определенном порядке, который повторяется в каждой строке исходной матрицы. Кажется, что этот числовой ряд действует аналогично музыкальной гамме, поскольку он определяет основной порядок музыкального произведения.

В склеенной матрице на определенных участках между строками соседних одинаковых чисел появляются синусоидальные волны. Эти синусоидальные волны могут двигаться вперед или назад относительно порядка исходного масштаба, они могут иметь разные длины волн и, кажется, меняют направление в строках, заполненных повторяющимися соседними числами. Мало того, эти гребни волн, по-видимому, также выполняют функцию переключения полярности волны. В объединенной матрице полярность означает, используют ли волны исходные столбцы сетки или столбцы из сетки, которую я перевернул по горизонтали и вставил в исходную матрицу.

В системе 13х20 масштаб всегда один и тот же: 1, 7, 13, 6, 12, 5, 11, 4, 10, 3, 9, 2, 6, 1 (все 6 цифр в 13-основном счете системы и которые, соединенные по кругу, кажется, создают узор, похожий на обмотку катушки) и которые можно увидеть ниже, регулярно меняющие «полярность» при движении от одного гребня волны к противоположному. 

Как упоминалось выше, обратите внимание, что в сетке 13x20, основанной на календаре Майя, каждый случай переключения полярности происходит либо на нижнем, либо на верхнем экстремуме волны.

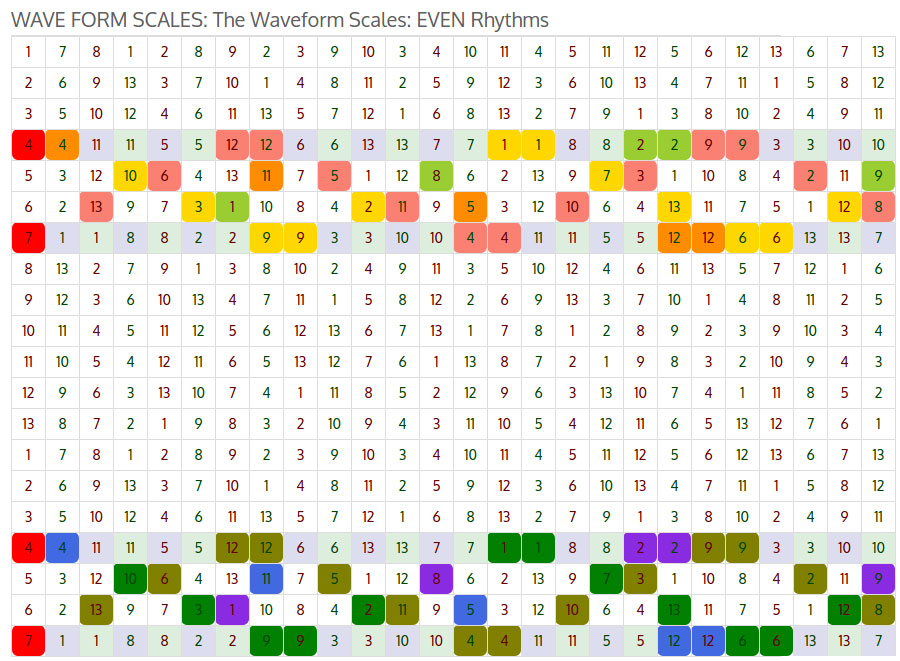
Сетка 13/20 с масштабом 1, 8, 2, 9, 3, 10, 4, 11, 5, 12, 6, 13, 7 

Я нашел эти закономерности необычными.

На цветных рисунках в сетке 13:20 синие пропорции, такие как числа (некоторые из которых неправильно отмечены на рисунке, который я отправил, но правильные в инструменте, с которым я связал вас выше), представляют дроби, обозначаемые тем, сколько целых чисел находится между каждое число в строке. Если вы заметили во вложении здесь, что отношения, созданные этими числами, все существуют вдоль диагональной линии Ламбдомной матрицы гармонических внутренних процессов.

Созданный мной инструмент выходит за рамки этого набора Цолькина майя (13/20) и может оценивать бесконечный набор пар чисел (в пределах пропускной способности моего сервера), а также генерирует расчеты гармоник, генерируемых в каждой строке. 

Как правило, ряды повторяющихся чисел имеют гармоники «нуля» или «бесконечности», когда синусоидальные волны меняют полярность и меняют направление на своих вершинах. Но я не хочу вам все портить, посмотрите сами!

Муаровые узоры: макроузоры, раскрывающие микроузоры

Вы когда-нибудь проезжали под пешеходным мостом? Когда вы находитесь под одним из этих мостов, узор, образовавшийся между двумя решетками, увеличит форму исходных отверстий, используемых в этих мостах.

Таким образом, муаровые узоры, кажется, усиливают основную реальность. Хитрость в том, что когда вы проходите под мостом, узоры между двумя решетками продолжают формироваться и меняться по мере того, как вы уходите под него.

Я начал рассматривать эти матрицы как своего рода муаровый узор, но хотел проверить свои предположения. В данном случае я специально хотел знать, что произойдет, если я сдвину две соединенные сетки вверх и вниз относительно друг друга. Сохранятся ли формы волн? Если да, то я предполагаю, что они усиливают и скрывают реальность, содержащуюся в исходных решетках.

Поэтому я создал компонент смещения, который вы можете увидеть в созданном мной инструменте. Оказывается, формы волн остаются неизменными.

На мой взгляд, это указывает на то, что эти склеенные сетки действительно обнаруживают феноменологическую последовательность, которая раскрывает кое-что об отношениях между этими двумя числами, используемыми для формирования сеток, и методами, использованными для создания самой склеенной сетки.

Генерируемые соотношения частот звука Ламбдомы

Эти частоты генерируются путем повторения соотношений между соседними числами. Из-за особенностей построения сеток вертикальные отношения вверх/вниз просто считают вверх и вниз, добавляя или вычитая на единицу.

Однако если вы считаете в любом другом направлении, используя собственную систему счета (основанную на меньшем числе, до которого подсчитывается при создании матриц), различия между соседними числами создают повторяющийся шаблон чисел, который также определяет соотношение, которое в оборот представляет собой частоту, которую можно вычислить в Гц. 

Ноты и частоты используют частотные диаграммы Пифагора Ламбдомы для определения соотношения с музыкальной гаммой.  

Поскольку коэффициенты должны иметь базовое число, по которому они рассчитываются, этой базе чаще всего присваивается значение 256 Гц или математически удобная для работы версия средней C. 

Но можно выбрать любую базовую частоту (представляющую значение 1). Инструмент, который я создал, позволяет пользователю выбирать любую базовую частоту, которую он хотел бы использовать в этих расчетах частот.

Это важно, потому что это, возможно, впервые позволяет формировать собранные ноты в музыкальные последовательности, которые можно накладывать друг на друга. 

Поскольку эти сгенерированные отношения могут быть установлены на любой частоте в качестве базовой, это позволяет проводить широкий спектр экспериментов со звуком в космосе и использовать инструмент для создания этих звуковых файлов. В настоящий момент меня особенно интересует эффект отмены и комбинации этих звуковых последовательностей и отношений в физическом пространстве.

Здесь можно услышать примеры частот календаря Майя:

Для комбинированных волн с базовой частотой 256 (6 слоев звука).

Здесь только для двух основных горизонтальных звуковых последовательностей (2 слоя звука).

Илья Орлов | Традиции | Практика | Исследования | Мастер - учитель Рэйки